Bounds for a conical surface, the opening angle is stored in \( \tan(\alpha) \) and always positively defined. More...

#include <Acts/Surfaces/ConeBounds.hpp>

Inheritance diagram for Acts::ConeBounds:

Collaboration diagram for Acts::ConeBounds:

Public Types
enum	BoundValues : int { eAlpha = 0 , eMinZ = 1 , eMaxZ = 2 , eHalfPhiSector = 3 , eAveragePhi = 4 , eSize = 5 }
	Enumeration for the bound values. More...
Public Types inherited from Acts::SurfaceBounds
enum	BoundsType : int { eCone = 0 , eCylinder = 1 , eDiamond = 2 , eDisc = 3 , eEllipse = 4 , eLine = 5 , eRectangle = 6 , eTrapezoid = 7 , eTriangle = 8 , eDiscTrapezoid = 9 , eConvexPolygon = 10 , eAnnulus = 11 , eBoundless = 12 , eOther = 13 }
	This is nested to the SurfaceBounds, as also VolumeBounds will have Bounds Type. More...

Public Member Functions
	ConeBounds (const std::array< double, eSize > &values) noexcept(false)
	Constructor - from parameters array.
	ConeBounds (double alpha, bool symm, double halfphi=std::numbers::pi, double avphi=0.) noexcept(false)
	Constructor - open cone with alpha, by default a full cone but optionally can make a conical section.
	ConeBounds (double alpha, double minz, double maxz, double halfphi=std::numbers::pi, double avphi=0.) noexcept(false)
	Constructor - open cone with alpha, minz and maxz, by default a full cone but can optionally make it a conical section.
SquareMatrix2	boundToCartesianJacobian (const Vector2 &lposition) const final
	Computes the bound to cartesian jacobian at a given local position.
SquareMatrix2	boundToCartesianMetric (const Vector2 &lposition) const final
	Computes the bound to cartesian metric at a given local position.
Vector2	center () const final
	Calculate the center of the surface bounds in local coordinates.
Vector2	closestPoint (const Vector2 &lposition, const SquareMatrix2 &metric) const final
	Calculates the closest point on the bounds to a given local position.
double	get (BoundValues bValue) const
	Access to the bound values.
bool	inside (const Vector2 &lposition) const final
	Inside check for the bounds object.
virtual bool	inside (const Vector2 &lposition, const BoundaryTolerance &boundaryTolerance) const
	Inside check for the bounds object given a boundary tolerance.
bool	isCartesian () const final
	Check if the bound coordinates are cartesian.
double	r (double z) const
	Return the radius at a specific z values.
double	tanAlpha () const
	Return tangent of alpha (pre-computed).
std::ostream &	toStream (std::ostream &sl) const final
	Output Method for std::ostream.
BoundsType	type () const final
	Return the bounds type - for persistency optimization.
std::vector< double >	values () const final
	Access method for bound values, this is a dynamically sized vector containing the parameters needed to describe these bounds.
Public Member Functions inherited from Acts::SurfaceBounds
virtual	~SurfaceBounds ()=default
virtual double	distance (const Vector2 &lposition) const
	Calculates the distance to the bounds from a given local position.

Detailed Description

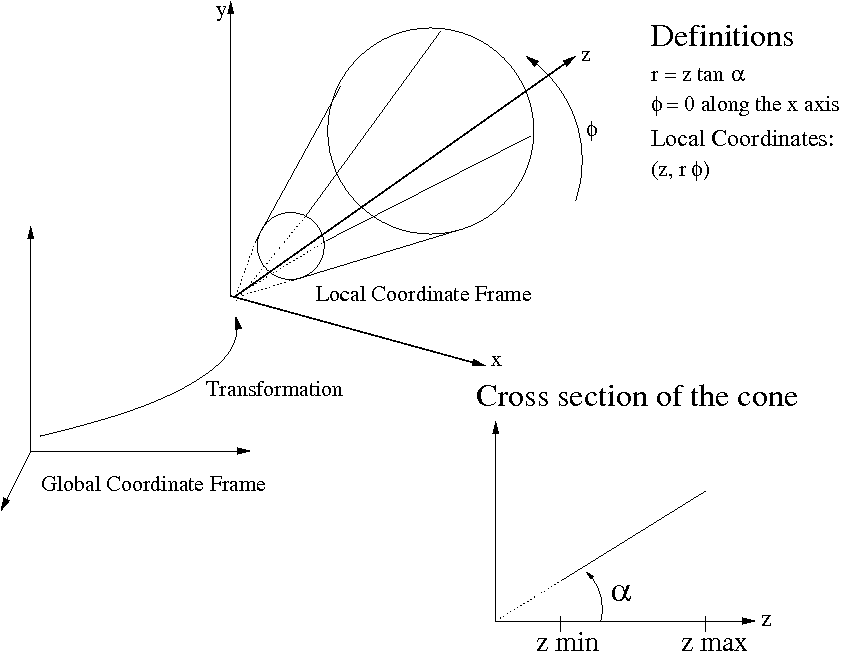
Bounds for a conical surface, the opening angle is stored in \( \tan(\alpha) \) and always positively defined.

The cone can open to both sides, steered by \( z_min \) and \( z_max \).

Member Enumeration Documentation

◆ BoundValues

enum Acts::ConeBounds::BoundValues : int

Enumeration for the bound values.

Enumerator
eAlpha
eMinZ
eMaxZ
eHalfPhiSector
eAveragePhi
eSize

Constructor & Destructor Documentation

◆ ConeBounds() [1/3]

Acts::ConeBounds::ConeBounds	(	double	alpha,
		bool	symm,
		double	halfphi = std::numbers::pi,
		double	avphi = 0. )

Constructor - open cone with alpha, by default a full cone but optionally can make a conical section.

Parameters

alpha	is the opening angle of the cone
symm	is the boolean indicating if the cone is symmetric in +/- z
halfphi	is the half opening angle (default is pi)
avphi	is the phi value around which the bounds are opened (default=0)

◆ ConeBounds() [2/3]

Acts::ConeBounds::ConeBounds	(	double	alpha,
		double	minz,
		double	maxz,
		double	halfphi = std::numbers::pi,
		double	avphi = 0. )

Constructor - open cone with alpha, minz and maxz, by default a full cone but can optionally make it a conical section.

Parameters

alpha	is the opening angle of the cone
minz	cone expanding from minimal z
maxz	cone expanding to maximal z
halfphi	is the half opening angle (default is pi)
avphi	is the phi value around which the bounds are opened (default=0)

◆ ConeBounds() [3/3]

Acts::ConeBounds::ConeBounds ( const std::array< double, eSize > & values )

explicit

Constructor - from parameters array.

Parameters

values The parameter array

Member Function Documentation

◆ boundToCartesianJacobian()

SquareMatrix2 Acts::ConeBounds::boundToCartesianJacobian ( const Vector2 & lposition ) const

finalvirtual

Computes the bound to cartesian jacobian at a given local position.

Parameters

lposition is the local position at which the jacobian is computed

Returns: the bound to cartesian jacobian

Implements Acts::SurfaceBounds.

◆ boundToCartesianMetric()

SquareMatrix2 Acts::ConeBounds::boundToCartesianMetric ( const Vector2 & lposition ) const

finalvirtual

Computes the bound to cartesian metric at a given local position.

Parameters

lposition is the local position at which the metric is computed

Returns: the bound to cartesian metric

Implements Acts::SurfaceBounds.

◆ center()

Vector2 Acts::ConeBounds::center ( ) const

finalvirtual

Calculate the center of the surface bounds in local coordinates.

This method returns a representative center point of the bounds region. The exact definition varies by bounds type and coordinate system:

Cartesian bounds (Rectangle, Diamond, Trapezoid):

Returns the geometric center or center of symmetry
For symmetric shapes: center of bounding box or origin (0,0)

Polar/Cylindrical bounds (Radial, Cylinder, Cone):

Returns (r, phi) where r is average radius, phi is average angle
Coordinates are in the bounds' natural coordinate system

Complex bounds (Annulus, ConvexPolygon):

Annulus: Pre-calculated from corner vertices (accounts for coordinate transforms)
Polygon: Average of all vertices (vertex centroid, not area centroid)

Infinite bounds: Returns conceptual center at (0,0)

Note: The returned point is guaranteed to be a reasonable representative center, but may not be the true geometric centroid for all shapes.

Returns: Vector2 representing the center position in local coordinates

Note: For ConeBounds: returns (averagePhi, (minZ + maxZ)/2) in cone coordinates

Implements Acts::SurfaceBounds.

◆ closestPoint()

Vector2 Acts::ConeBounds::closestPoint	(	const Vector2 &	lposition,
		const SquareMatrix2 &	metric ) const

finalvirtual

Calculates the closest point on the bounds to a given local position.

Parameters

lposition	is the local position
metric	to be used for the distance calculation

Returns: the closest point on the bounds

Implements Acts::SurfaceBounds.

◆ get()

double Acts::ConeBounds::get ( BoundValues bValue ) const

Access to the bound values.

Parameters

bValue the class nested enum for the array access

Returns: Value of the specified bound parameter

◆ inside() [1/2]

bool Acts::ConeBounds::inside ( const Vector2 & lposition ) const

finalvirtual

Inside check for the bounds object.

Parameters

lposition is the local position

Returns: true if the local position is inside the bounds

Implements Acts::SurfaceBounds.

◆ inside() [2/2]

virtual bool Acts::SurfaceBounds::inside	(	const Vector2 &	lposition,
		const BoundaryTolerance &	boundaryTolerance ) const

virtual

Inside check for the bounds object given a boundary tolerance.

Parameters

lposition	is the local position
boundaryTolerance	is the boundary tolerance object

Returns: true if the local position is inside the bounds and tolerance

Reimplemented from Acts::SurfaceBounds.

◆ isCartesian()

bool Acts::ConeBounds::isCartesian ( ) const

finalvirtual

Check if the bound coordinates are cartesian.

Returns: true if the bound coordinates are cartesian

Implements Acts::SurfaceBounds.

◆ r()

double Acts::ConeBounds::r ( double z ) const

Return the radius at a specific z values.

Parameters

z	is the z value for which r is requested

Returns: is the r value associated with z

◆ tanAlpha()

double Acts::ConeBounds::tanAlpha ( ) const

Return tangent of alpha (pre-computed).

Returns: Tangent of the cone half-angle

◆ toStream()

std::ostream & Acts::ConeBounds::toStream ( std::ostream & sl ) const

finalvirtual

Output Method for std::ostream.

Parameters

sl	is the ostrea into which the dump is done

Returns: is the input object

Implements Acts::SurfaceBounds.

◆ type()

BoundsType Acts::ConeBounds::type ( ) const

finalvirtual

Return the bounds type - for persistency optimization.

Returns: the bounds type

Implements Acts::SurfaceBounds.

◆ values()

std::vector< double > Acts::ConeBounds::values ( ) const

finalvirtual

Access method for bound values, this is a dynamically sized vector containing the parameters needed to describe these bounds.

Returns: of the stored values for this SurfaceBounds object

Implements Acts::SurfaceBounds.

Public Types

Public Member Functions

Detailed Description

Member Enumeration Documentation

◆ BoundValues

Constructor & Destructor Documentation

◆ ConeBounds() [1/3]

◆ ConeBounds() [2/3]

◆ ConeBounds() [3/3]

Member Function Documentation

◆ boundToCartesianJacobian()

◆ boundToCartesianMetric()

◆ center()

◆ closestPoint()

◆ get()

◆ inside() [1/2]

◆ inside() [2/2]

◆ isCartesian()

◆ r()

◆ tanAlpha()

◆ toStream()

◆ type()

◆ values()