Base class for a linear surfaces in the TrackingGeometry to describe dirft tube, straw like detectors or the Perigee It inherits from Surface. More...

#include <Acts/Surfaces/LineSurface.hpp>

Inheritance diagram for Acts::LineSurface:

[legend]

Collaboration diagram for Acts::LineSurface:

[legend]

Public Member Functions
AlignmentToPathMatrix	alignmentToPathDerivative (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
	Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.
void	assignSurfaceBounds (std::shared_ptr< const LineBounds > newBounds)
	Overwrite the existing surface bounds with new ones.
const SurfaceBounds &	bounds () const final
	This method returns the bounds of the surface by reference.
const std::shared_ptr< const LineBounds > &	boundsPtr () const
	This method returns the shared_ptr to the LineBounds.
BoundToFreeMatrix	boundToFreeJacobian (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
	Calculate the jacobian from local to global which the surface knows best, hence the calculation is done here.
FreeToPathMatrix	freeToPathDerivative (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
	Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.
Result< Vector2 >	globalToLocal (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance=s_onSurfaceTolerance) const final
	Specified for LineSurface: global to local method without dynamic memory allocation.
MultiIntersection3D	intersect (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryTolerance &boundaryTolerance=BoundaryTolerance::Infinite(), double tolerance=s_onSurfaceTolerance) const final
	Calculate the straight-line intersection with the line surface.
Vector3	lineDirection (const GeometryContext &gctx) const
	Get the line direction in global coordinates.
ActsMatrix< 2, 3 >	localCartesianToBoundLocalDerivative (const GeometryContext &gctx, const Vector3 &position) const final
	Calculate the derivative of bound track parameters local position w.r.t.
Vector3	localToGlobal (const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const final
	Local to global transformation.
std::string	name () const override
	Return properly formatted class name for screen output.
Vector3	normal (const GeometryContext &gctx, const Vector3 &pos, const Vector3 &direction) const override
	Return the surface normal at a given `position` and `direction`.
LineSurface &	operator= (const LineSurface &other)
	Assignment operator.
double	pathCorrection (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const override
	the pathCorrection for derived classes with thickness is by definition 1 for LineSurfaces
RotationMatrix3	referenceFrame (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
	Return the measurement frame - this is needed for alignment, in particular.
Vector3	referencePosition (const GeometryContext &gctx, AxisDirection aDir) const final
	The binning position is the position calculated for a certain binning type.
Public Member Functions inherited from Acts::Surface
	~Surface () noexcept override
AlignmentToBoundMatrix	alignmentToBoundDerivative (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const FreeVector &pathDerivative) const
	The derivative of bound track parameters w.r.t.
void	assignDetectorElement (const SurfacePlacementBase &detelement)
	Assign a detector element.
void	assignIsSensitive (bool isSensitive)
	Assign whether the surface is sensitive.
void	assignSurfaceMaterial (std::shared_ptr< const ISurfaceMaterial > material)
	Assign the surface material description.
void	assignSurfacePlacement (const SurfacePlacementBase &placement)
	Assign a placement object which may dynamically align the surface in space.
void	assignThickness (double thick)
	Assign the thickness of the surface in the orthogonal dimension.
const DetectorElementBase *	associatedDetectorElement () const
	Return method for the associated Detector Element.
const Layer *	associatedLayer () const
	Return method for the associated Layer in which the surface is embedded.
void	associateLayer (const Layer &lay)
	Set Associated Layer Many surfaces can be associated to a Layer, but it might not be known yet during construction of the layer, this can be set afterwards.
virtual Vector3	center (const GeometryContext &gctx) const
	Return method for the surface center.
virtual Vector2	closestPointOnBoundary (const Vector2 &lposition, const SquareMatrix2 &metric) const
	Calculates the closest point on the boundary of the surface to a given point in local coordinates.
virtual double	distanceToBoundary (const Vector2 &lposition) const
	Calculates the distance to the boundary of the surface from a given point in local coordinates.
virtual FreeToBoundMatrix	freeToBoundJacobian (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const
	Calculate the jacobian from global to local which the surface knows best, hence the calculation is done here.
std::shared_ptr< Surface >	getSharedPtr ()
	Retrieve a `std::shared_ptr` for this surface (non-const version).
std::shared_ptr< const Surface >	getSharedPtr () const
	Retrieve a `std::shared_ptr` for this surface (const version).
virtual bool	insideBounds (const Vector2 &lposition, const BoundaryTolerance &boundaryTolerance=BoundaryTolerance::None()) const
	The insideBounds method for local positions.
bool	isAlignable () const
	Returns whether the Surface is alignable.
bool	isOnSurface (const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryTolerance &boundaryTolerance=BoundaryTolerance::None(), double tolerance=s_onSurfaceTolerance) const
	The geometric onSurface method.
bool	isSensitive () const
	Returns whether the Surface is sensitive.
const Transform3 &	localToGlobalTransform (const GeometryContext &gctx) const
	Return method for the surface Transform3 by reference In case a detector element is associated the surface transform is just forwarded to the detector element in order to keep the (mis-)alignment cache cetrally handled.
Surface &	operator= (const Surface &other)
	Assignment operator.
bool	operator== (const Surface &other) const
	Comparison (equality) operator The strategy for comparison is (a) first pointer comparison (b) then type comparison (c) then bounds comparison (d) then transform comparison.
virtual Polyhedron	polyhedronRepresentation (const GeometryContext &gctx, unsigned int quarterSegments=2u) const =0
	Return a Polyhedron for surface objects.
const ISurfaceMaterial *	surfaceMaterial () const
	Return method for the associated Material to this surface.
const std::shared_ptr< const ISurfaceMaterial > &	surfaceMaterialSharedPtr () const
	Return method for the shared pointer to the associated Material.
const SurfacePlacementBase *	surfacePlacement () const
	Return the associated surface placement if there is any.
double	thickness () const
	Return the thickness of the surface in the normal direction.
GeometryContextOstreamWrapper< Surface >	toStream (const GeometryContext &gctx) const
	Helper method for printing: the returned object captures the surface and the geometry context and will print the surface.
std::string	toString (const GeometryContext &gctx) const
	Output into a std::string.
const Transform3 &	transform (const GeometryContext &gctx) const
	Return method for the surface Transform3 by reference In case a detector element is associated the surface transform is just forwarded to the detector element in order to keep the (mis-)alignment cache cetrally handled.
virtual SurfaceType	type () const =0
	Return method for the Surface type to avoid dynamic casts.
void	visualize (IVisualization3D &helper, const GeometryContext &gctx, const ViewConfig &viewConfig=s_viewSurface) const
	Visualize the surface for debugging and inspection.
Public Member Functions inherited from Acts::GeometryObject
	GeometryObject ()=default
	Defaulted constructor.
	GeometryObject (const GeometryIdentifier &geometryId)
	Constructor from a value.
	GeometryObject (const GeometryObject &)=default
	Defaulted copy constructor.
virtual	~GeometryObject () noexcept=default
void	assignGeometryId (const GeometryIdentifier &geometryId)
	Set the value.
GeometryIdentifier	geometryId () const
virtual double	referencePositionValue (const GeometryContext &gctx, AxisDirection aDir) const
	Implement the binningValue.

Protected Member Functions
	LineSurface (const GeometryContext &gctx, const LineSurface &other, const Transform3 &shift)
	Copy constructor - with shift.
	LineSurface (const LineSurface &other)
	Copy constructor.
	LineSurface (const Transform3 &transform, double radius, double halez)
	Constructor for LineSurface from Transform3 and radial dimensions.
	LineSurface (const Transform3 &transform, std::shared_ptr< const LineBounds > lbounds=nullptr)
	Constructor for LineSurface from Transform3 and LineBounds.
	LineSurface (std::shared_ptr< const LineBounds > lbounds, const SurfacePlacementBase &placement)
	Constructor from SurfacePlacementBase : Element proxy.
Protected Member Functions inherited from Acts::Surface
	Surface (const GeometryContext &gctx, const Surface &other, const Transform3 &shift) noexcept
	Copy constructor with optional shift.
	Surface (const Surface &other) noexcept
	Copy constructor.
	Surface (const SurfacePlacementBase &placement) noexcept
	Constructor from SurfacePlacement: Element proxy.
	Surface (const Transform3 &transform=Transform3::Identity())
	Constructor with Transform3 as a shared object.
virtual std::ostream &	toStreamImpl (const GeometryContext &gctx, std::ostream &sl) const
	Output Method for std::ostream, to be overloaded by child classes.

Protected Attributes
std::shared_ptr< const LineBounds >	m_bounds
	bounds (shared)
Protected Attributes inherited from Acts::Surface
std::unique_ptr< const Transform3 >	m_transform {}
	Transform3 definition that positions (translation, rotation) the surface in global space.
Protected Attributes inherited from Acts::GeometryObject
GeometryIdentifier	m_geometryId
	Unique geometry identifier for this object.

Additional Inherited Members
Public Types inherited from Acts::Surface
enum	SurfaceType { Cone = 0 , Cylinder = 1 , Disc = 2 , Perigee = 3 , Plane = 4 , Straw = 5 , Curvilinear = 6 , Other = 7 }
	This enumerator simplifies the persistency & calculations, by saving a dynamic_cast, e.g. More...
Static Public Member Functions inherited from Acts::Surface
template<class T, typename... Args>
static std::shared_ptr< T >	makeShared (Args &&... args)
	Factory for producing memory managed instances of Surface.
Static Public Attributes inherited from Acts::Surface
static constexpr std::array< std::string_view, Surface::SurfaceType::Other+1 >	s_surfaceTypeNames
	Helper strings for screen output.

Detailed Description

Base class for a linear surfaces in the TrackingGeometry to describe dirft tube, straw like detectors or the Perigee It inherits from Surface.

Note: It leaves the type() method virtual, so it can not be instantiated

Constructor & Destructor Documentation

◆ LineSurface() [1/5]

Acts::LineSurface::LineSurface	(	const Transform3 &	transform,
		double	radius,
		double	halez )

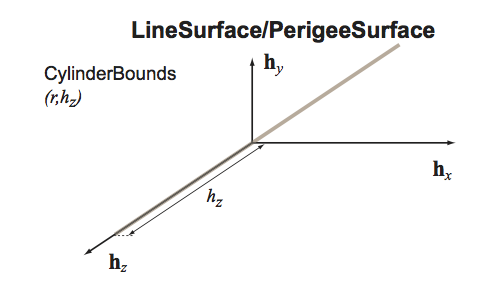
explicitprotected

Constructor for LineSurface from Transform3 and radial dimensions.

Parameters

transform	The transform that positions the line in the global frame
radius	The radius of the line
halez	The half length in z

◆ LineSurface() [2/5]

Acts::LineSurface::LineSurface	(	const Transform3 &	transform,
		std::shared_ptr< const LineBounds >	lbounds = nullptr )

explicitprotected

Constructor for LineSurface from Transform3 and LineBounds.

Parameters

transform	The transform that positions the line in the global frame
lbounds	The bounds describing the line dimensions

◆ LineSurface() [3/5]

Acts::LineSurface::LineSurface	(	std::shared_ptr< const LineBounds >	lbounds,
		const SurfacePlacementBase &	placement )

explicitprotected

Constructor from SurfacePlacementBase : Element proxy.

Parameters

lbounds	are the bounds describing the line dimensions, they must not be nullptr
placement	Reference to the surface placement

Note: The Surface does not take any ownership over the SurfacePlacementBase it is expected that the user ensures the life-time of the SurfacePlacementBase and that the Surface is actually owned by the SurfacePlacementBase instance

◆ LineSurface() [4/5]

Acts::LineSurface::LineSurface ( const LineSurface & other )

protected

Copy constructor.

Parameters

other The source surface for copying

◆ LineSurface() [5/5]

Acts::LineSurface::LineSurface	(	const GeometryContext &	gctx,
		const LineSurface &	other,
		const Transform3 &	shift )

explicitprotected

Copy constructor - with shift.

Parameters

gctx	The current geometry context object, e.g. alignment
other	is the source cone surface
shift	is the additional transform applied after copying

Member Function Documentation

◆ alignmentToPathDerivative()

AlignmentToPathMatrix Acts::LineSurface::alignmentToPathDerivative	(	const GeometryContext &	gctx,
		const Vector3 &	position,
		const Vector3 &	direction ) const

finalvirtual

Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.

alignment parameters of the surface (i.e. local frame origin in global 3D Cartesian coordinates and its rotation represented with extrinsic Euler angles)

Parameters

gctx	The current geometry context object, e.g. alignment
position	global 3D position
direction	global 3D momentum direction

Returns: Derivative of path length w.r.t. the alignment parameters

Reimplemented from Acts::Surface.

◆ assignSurfaceBounds()

void Acts::LineSurface::assignSurfaceBounds ( std::shared_ptr< const LineBounds > newBounds )

Overwrite the existing surface bounds with new ones.

Parameters

newBounds Pointer to the new bounds

◆ bounds()

const SurfaceBounds & Acts::LineSurface::bounds ( ) const

finalvirtual

This method returns the bounds of the surface by reference.

Returns: Reference to the surface bounds

Implements Acts::Surface.

◆ boundsPtr()

const std::shared_ptr< const LineBounds > & Acts::LineSurface::boundsPtr ( ) const

This method returns the shared_ptr to the LineBounds.

◆ boundToFreeJacobian()

BoundToFreeMatrix Acts::LineSurface::boundToFreeJacobian	(	const GeometryContext &	gctx,
		const Vector3 &	position,
		const Vector3 &	direction ) const

finalvirtual

Calculate the jacobian from local to global which the surface knows best, hence the calculation is done here.

Parameters

gctx	The current geometry context object, e.g. alignment
position	global 3D position
direction	global 3D momentum direction

Returns: Jacobian from local to global

Reimplemented from Acts::Surface.

◆ freeToPathDerivative()

FreeToPathMatrix Acts::LineSurface::freeToPathDerivative	(	const GeometryContext &	gctx,
		const Vector3 &	position,
		const Vector3 &	direction ) const

finalvirtual

Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.

free parameters

Parameters

gctx	The current geometry context object, e.g. alignment
position	global 3D position
direction	global 3D momentum direction

Returns: Derivative of path length w.r.t. free parameters

Reimplemented from Acts::Surface.

◆ globalToLocal()

Result< Vector2 > Acts::LineSurface::globalToLocal	(	const GeometryContext &	gctx,
		const Vector3 &	position,
		const Vector3 &	direction,
		double	tolerance = s_onSurfaceTolerance ) const

finalvirtual

Specified for LineSurface: global to local method without dynamic memory allocation.

This method is the true global -> local transformation. It makes use of globalToLocal and indicates the sign of the Acts::eBoundLoc0 by the given momentum direction.

The calculation of the sign of the radius (or \( d_0 \)) can be done as follows: May \( \vec d = \vec m - \vec c \) denote the difference between the center of the line and the global position of the measurement/predicted state. Then, \( \vec d \) lies in the so-called measurement plane. The latter is determined by the two orthogonal vectors \(\vec{\texttt{measY}} = \vec{e}_z \) and \(\vec{\texttt{measX}} = \vec{\texttt{measY}} \times \frac{\vec{p}}{|\vec{p}|} \).

The sign of the radius (or \( d_{0} \) ) is then defined by the projection of \( \vec{d} \) on \( \vec{measX} \):
\( sign = -sign(\vec{d} \cdot \vec{measX}) \)

Parameters

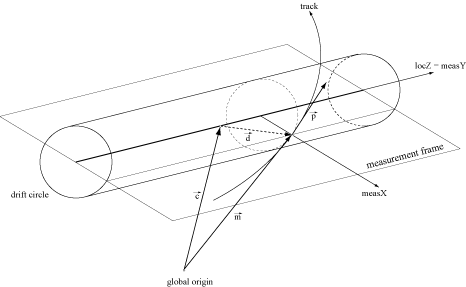
gctx	The current geometry context object, e.g. alignment
position	global 3D position - considered to be on surface but not inside bounds (check is done)
direction	global 3D momentum direction (optionally ignored)
tolerance	(unused)

Returns: A Result<Vector2>, which is set to !ok() if the position is not the point of closest approach to the line surface.

Implements Acts::Surface.

◆ intersect()

MultiIntersection3D Acts::LineSurface::intersect	(	const GeometryContext &	gctx,
		const Vector3 &	position,
		const Vector3 &	direction,
		const BoundaryTolerance &	boundaryTolerance = BoundaryTolerance::Infinite(),
		double	tolerance = s_onSurfaceTolerance ) const

finalvirtual

Calculate the straight-line intersection with the line surface.

Mathematical motivation:

Given two lines in parametric form:

\( \vec l_{a}(u) = \vec m_a + u \cdot \vec e_{a} \)

\( \vec l_{b}(\mu) = \vec m_b + \mu \cdot \vec e_{b} \)

The vector between any two points on the two lines is given by:

\( \vec s(u, \mu) = \vec l_{b} - l_{a} = \vec m_{ab} + \mu \cdot \vec e_{b} - u \cdot \vec e_{a} \),

where \( \vec m_{ab} = \vec m_{b} - \vec m_{a} \).

\( \vec s(u_0, \mu_0) \) denotes the vector between the two closest points

\( \vec l_{a,0} = l_{a}(u_0) \) and \( \vec l_{b,0} = l_{b}(\mu_0) \)

and is perpendicular to both, \( \vec e_{a} \) and \( \vec e_{b} \).

This results in a system of two linear equations:

(i) \( 0 = \vec s(u_0, \mu_0) \cdot \vec e_a = \vec m_{ab} \cdot \vec e_a + \mu_0 \vec e_a \cdot \vec e_b - u_0 \)
(ii) \( 0 = \vec s(u_0, \mu_0) \cdot \vec e_b = \vec m_{ab} \cdot \vec e_b + \mu_0 - u_0 \vec e_b \cdot \vec e_a \)

Solving (i) and (ii) for \( u \) and \( \mu_0 \) yields:

\( u_0 = \frac{(\vec m_{ab} \cdot \vec e_a)-(\vec m_{ab} \cdot \vec e_b)(\vec e_a \cdot \vec e_b)}{1-(\vec e_a \cdot \vec e_b)^2} \)
\( \mu_0 = - \frac{(\vec m_{ab} \cdot \vec e_b)-(\vec m_{ab} \cdot \vec e_a)(\vec e_a \cdot \vec e_b)}{1-(\vec e_a \cdot \vec e_b)^2} \)

The function checks if \( u_0 \simeq 0\) to check if the current position is at the point of closest approach, i.e. the intersection point, in which case it will return an onSurace intersection result. Otherwise, the path length from position to the point of closest approach ( \( u_0 \)) is returned in a reachable intersection.

Parameters

gctx	The current geometry context object, e.g. alignment
position	The global position as a starting point
direction	The global direction at the starting point

Note: expected to be normalized

Parameters

boundaryTolerance	The boundary check directive for the estimate
tolerance	the tolerance used for the intersection

Returns: is the intersection object

Implements Acts::Surface.

◆ lineDirection()

Vector3 Acts::LineSurface::lineDirection ( const GeometryContext & gctx ) const

Get the line direction in global coordinates.

Parameters

gctx	The geometry context

Returns: The direction vector of the line surface

◆ localCartesianToBoundLocalDerivative()

ActsMatrix< 2, 3 > Acts::LineSurface::localCartesianToBoundLocalDerivative	(	const GeometryContext &	gctx,
		const Vector3 &	position ) const

finalvirtual

Calculate the derivative of bound track parameters local position w.r.t.

position in local 3D Cartesian coordinates

Parameters

gctx	The current geometry context object, e.g. alignment
position	The position of the parameters in global

Returns: Derivative of bound local position w.r.t. position in local 3D cartesian coordinates

Implements Acts::Surface.

◆ localToGlobal()

Vector3 Acts::LineSurface::localToGlobal	(	const GeometryContext &	gctx,
		const Vector2 &	lposition,
		const Vector3 &	direction ) const

finalvirtual

Local to global transformation.

Note: for line surfaces the momentum direction is used in order to interpret the drift radius

Parameters

gctx	The current geometry context object, e.g. alignment
lposition	is the local position to be transformed
direction	is the global momentum direction (used to sign the closest approach)

Returns: global position by value

Implements Acts::Surface.

◆ name()

std::string Acts::LineSurface::name ( ) const

overridevirtual

Return properly formatted class name for screen output.

Returns: String representation of the class name

Implements Acts::Surface.

Reimplemented in Acts::PerigeeSurface, and Acts::StrawSurface.

◆ normal()

Vector3 Acts::LineSurface::normal	(	const GeometryContext &	gctx,
		const Vector3 &	pos,
		const Vector3 &	direction ) const

overridevirtual

Return the surface normal at a given position and direction.

This method is fully generic, and valid for all surface types.

Note: For some surface types, the direction is ignored, but it is not safe to pass in a zero vector!

Parameters

gctx	The current geometry context object, e.g. alignment
pos	The position at which to calculate the normal
direction	The direction at which to calculate the normal

Returns: The normal vector at the given position and direction

Implements Acts::Surface.

◆ operator=()

LineSurface & Acts::LineSurface::operator= ( const LineSurface & other )

Assignment operator.

Parameters

other is the source surface dor copying

Returns: Reference to this LineSurface after assignment

◆ pathCorrection()

double Acts::LineSurface::pathCorrection	(	const GeometryContext &	gctx,
		const Vector3 &	position,
		const Vector3 &	direction ) const

overridevirtual

the pathCorrection for derived classes with thickness is by definition 1 for LineSurfaces

Parameters

gctx	Geometry context (ignored)
position	Position parameter (ignored)
direction	Direction parameter (ignored)

Note: input parameters are ignored; there's no material associated to the line surface

Returns: Always returns 1.0 for line surfaces

Implements Acts::Surface.

◆ referenceFrame()

RotationMatrix3 Acts::LineSurface::referenceFrame	(	const GeometryContext &	gctx,
		const Vector3 &	position,
		const Vector3 &	direction ) const

finalvirtual

Return the measurement frame - this is needed for alignment, in particular.

for StraightLine and Perigee Surface

the default implementation is the RotationMatrix3 of the transform

Parameters

gctx	The current geometry context object, e.g. alignment
position	is the global position where the measurement frame is constructed
direction	is the momentum direction used for the measurement frame construction

Returns: is a rotation matrix that indicates the measurement frame

Reimplemented from Acts::Surface.

◆ referencePosition()

Vector3 Acts::LineSurface::referencePosition	(	const GeometryContext &	gctx,
		AxisDirection	aDir ) const

finalvirtual

The binning position is the position calculated for a certain binning type.

Parameters

gctx	The current geometry context object, e.g. alignment
aDir	is the axis direction for the reference position request

Returns: position that can beused for this binning

Implements Acts::GeometryObject.

Member Data Documentation

◆ m_bounds

std::shared_ptr<const LineBounds> Acts::LineSurface::m_bounds

protected

bounds (shared)

Public Member Functions

Protected Member Functions

Protected Attributes

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

◆ LineSurface() [1/5]

◆ LineSurface() [2/5]

◆ LineSurface() [3/5]

◆ LineSurface() [4/5]

◆ LineSurface() [5/5]

Member Function Documentation

◆ alignmentToPathDerivative()

◆ assignSurfaceBounds()

◆ bounds()

◆ boundsPtr()

◆ boundToFreeJacobian()

◆ freeToPathDerivative()

◆ globalToLocal()

◆ intersect()

◆ lineDirection()

◆ localCartesianToBoundLocalDerivative()

◆ localToGlobal()

◆ name()

◆ normal()

◆ operator=()

◆ pathCorrection()

◆ referenceFrame()

◆ referencePosition()

Member Data Documentation

◆ m_bounds